Monday, January 16, 2012

Matrix Operations



Before we give the formal definition of how to multiply two matrices, we will discuss an example from a real life situation. Consider a city with two kinds of population: the inner city population and the suburb population. We assume that every year 40% of the inner city population moves to the suburbs, while 30% of the suburb population moves to the inner part of the city. Let I (resp. S) be the initial population of the inner city (resp. the suburban area). So after one year, the population of the inner part is


0.6 I + 0.3 S


while the population of the suburbs is

0.4 I + 0.7 S


After two years, the population of the inner city is

0.6 (0.6 I + 0.3 S) + 0.3 (0.4 I + 0.7 S)


and the suburban population is given by

0.4 (0.6 I + 0.3 S) + 0.7(0.4 I + 0.7 S)

Blue Matrix 1 Myspace Layout 2.0

Is there a nice way of representing the two populations after a certain number of years? Let us show how matrices may be helpful to answer this question. Let us represent the two populations in one table (meaning a column object with two entries):

\begin{displaymath}\left(\begin{array}{c} I\\ S\\ \end{array}\right)\end{displaymath}


So after one year the table which gives the two populations is

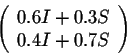
\begin{displaymath}\left(\begin{array}{c} 0.6 I + 0.3 S\\ 0.4 I + 0.7 S\\ \end{array}\right)\end{displaymath}


If we consider the following rule (the product of two matrices)

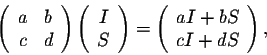
\begin{displaymath}\left(\begin{array}{cc} a&b\\ c&d\\ \end{array}\right) \lef... ...left(\begin{array}{c} aI + bS\\ cI + dS\\ \end{array}\right),\end{displaymath}


then the populations after one year are given by the formula

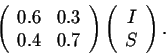
\begin{displaymath}\left(\begin{array}{cc} 0.6&0.3\\ 0.4&0.7\\ \end{array}\right) \left(\begin{array}{c} I\\ S\\ \end{array}\right).\end{displaymath}


After two years the populations are

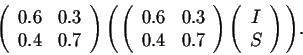
\begin{displaymath}\left(\begin{array}{cc} 0.6&0.3\\ 0.4&0.7\\ \end{array}\rig... ...ght) \left(\begin{array}{c} I\\ S\\ \end{array}\right)\Bigg).\end{displaymath}


Combining this formula with the above result, we get

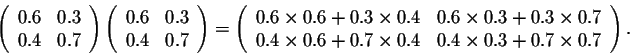
\begin{displaymath}\left(\begin{array}{cc} 0.6&0.3\\ 0.4&0.7\\ \end{array}\rig... ...imes 0.4&0.4 \times 0.3 + 0.7 \times0.7\\ \end{array}\right). \end{displaymath}


In other words, we have

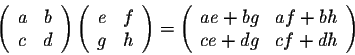
\begin{displaymath}\left(\begin{array}{cc} a&b\\ c&d\\ \end{array}\right) \lef... ...{array}{cc} ae+ bg&af+bh\\ ce + dg&cf+dh\\ \end{array}\right)\end{displaymath}

In fact, we do not need to have two matrices of the same size to multiply them. Above, we did multiply a (2x2) matrix with a (2x1) matrix (which gave a (2x1) matrix). In fact, the general rule says that in order to perform the multiplication AB, where A is a (mxn) matrix and B a (kxl) matrix, then we must have n=k. The result will be a (mxl) matrix. For example, we have

\begin{displaymath}\left(\begin{array}{ccc} a&b&c\\ d&e&f\\ \end{array}\right)... ...a +b\beta +c\nu\\ d\alpha +e\beta +f\nu\\ \end{array}\right).\end{displaymath}


Remember that though we were able to perform the above multiplication, it is not possible to perform the multiplication

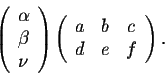
\begin{displaymath}\left(\begin{array}{c} \alpha\\ \beta\\ \nu\\ \end{array}\... ...)\left(\begin{array}{ccc} a&b&c\\ d&e&f\\ \end{array}\right).\end{displaymath}


So we have to be very careful about multiplying matrices. Sentences like "multiply the two matrices A and B" do not make sense. You must know which of the two matrices will be to the right (of your multiplication) and which one will be to the left; in other words, we have to know whether we are asked to perform $A \times B$ or $B \times A$. Even if both multiplications do make sense (as in the case of square matrices with the same size), we still have to be very careful. Indeed, consider the two matrices

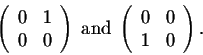
\begin{displaymath}\left(\begin{array}{cc} 0&1\\ 0&0\\ \end{array}\right)\;\mb... ...nd}\; \left(\begin{array}{cc} 0&0\\ 1&0\\ \end{array}\right).\end{displaymath}


We have

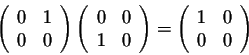
\begin{displaymath}\left(\begin{array}{cc} 0&1\\ 0&0\\ \end{array}\right)\left... ...ht) = \left(\begin{array}{cc} 1&0\\ 0&0\\ \end{array}\right) \end{displaymath}


and

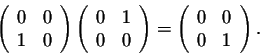
\begin{displaymath}\left(\begin{array}{cc} 0&0\\ 1&0\\ \end{array}\right)\left... ...ht) = \left(\begin{array}{cc} 0&0\\ 0&1\\ \end{array}\right).\end{displaymath}


So what is the conclusion behind this example? The matrix multiplication is not commutative, the order in which matrices are multiplied is important. In fact, this little setback is a major problem in playing around with matrices. This is something that you must always be careful with. Let us show you another setback. We have

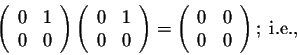
\begin{displaymath}\left(\begin{array}{cc} 0&1\\ 0&0\\ \end{array}\right)\left... ...egin{array}{cc} 0&0\\ 0&0\\ \end{array}\right);\;\mbox{i.e.},\end{displaymath}


the product of two non-zero matrices may be equal to the zero-matrix.




Properties involving Addition. Let A, B, and C be mxn matrices. We have
1.
A+B = B+A
2.
(A+B)+C = A + (B+C)
3.
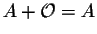
$A + {\cal O} = A$
where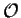 $\cal O$ is the mxn zero-matrix (all its entries are equal to 0);
4.
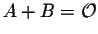$A+B = {\cal O}$ if and only if B = -A.

Properties involving Multiplication.

1.
Let A, B, and C be three matrices. If you can perform the products AB, (AB)C, BC, and A(BC), then we have

(AB)C = A (BC)


Note, for example, that if A is 2x3, B is 3x3, and C is 3x1, then the above products are possible (in this case, (AB)C is 2x1 matrix).
2.
If $\alpha$ and $\beta$ are numbers, and A is a matrix, then we have

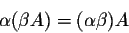
\begin{displaymath}\alpha (\beta A) = (\alpha \beta) A\end{displaymath}


3.
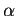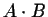If $\alpha$ is a number, and A and B are two matrices such that the product $A\cdot B$ is possible, then we have

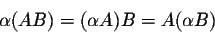
\begin{displaymath}\alpha (AB) = (\alpha A)B = A (\alpha B)\end{displaymath}


4.
If A is an nxm matrix and 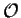$\cal O$ the mxk zero-matrix, then

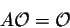
\begin{displaymath}A {\cal O} = {\cal O}\end{displaymath}


Note that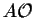 $A {\cal O}$ is the nxk zero-matrix. So if n is different from m, the two zero-matrices are different.

Properties involving Addition and Multiplication.
1.
Let A, B, and C be three matrices. If you can perform the appropriate products, then we have

(A+B)C = AC + BC


and

A(B+C) = AB + AC


2.
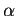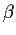If $\alpha$ and $\beta$ are numbers, A and B are matrices, then we have

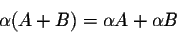
\begin{displaymath}\alpha (A+B) = \alpha A + \alpha B\end{displaymath}


and

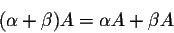
\begin{displaymath}(\alpha +\beta)A = \alpha A + \beta B\end{displaymath}


Example. Consider the matrices



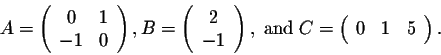
\begin{displaymath}A = \left(\begin{array}{cc} 0&1\\ -1&0\\ \end{array}\right)... ...nd}\; C = \left(\begin{array}{ccc} 0&1&5\\ \end{array}\right).\end{displaymath}



Evaluate (AB)C and A(BC). Check that you get the same matrix.
Answer. We have



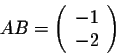
\begin{displaymath}AB = \left(\begin{array}{c} -1\\ -2\\ \end{array}\right)\end{displaymath}



so



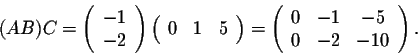
\begin{displaymath}(AB)C = \left(\begin{array}{c} -1\\ -2\\ \end{array}\right)... ...t(\begin{array}{ccc} 0&-1&-5\\ 0&-2&-10\\ \end{array}\right).\end{displaymath}



On the other hand, we have



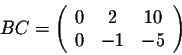
\begin{displaymath}BC = \left(\begin{array}{ccc} 0&2&10\\ 0&-1&-5\\ \end{array}\right)\end{displaymath}



so



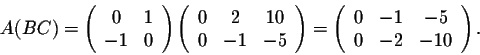
\begin{displaymath}A(BC) = \left(\begin{array}{cc} 0&1\\ -1&0\\ \end{array}\ri... ...t(\begin{array}{ccc} 0&-1&-5\\ 0&-2&-10\\ \end{array}\right).\end{displaymath}




Example. Consider the matrices



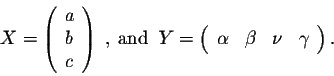
\begin{displaymath}X = \left(\begin{array}{c} a\\ b\\ c\\ \end{array}\right)\... ...ray}{cccc} \alpha & \beta & \nu & \gamma\\ \end{array}\right).\end{displaymath}



It is easy to check that



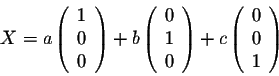
\begin{displaymath}X = a \left(\begin{array}{c} 1\\ 0\\ 0\\ \end{array}\right... ...) + c \left(\begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right) \end{displaymath}



and



\begin{displaymath}Y = \alpha \left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ \end{ar... ...ma \left(\begin{array}{cccc} 0 &0 & 0& 1\\ \end{array}\right).\end{displaymath}



These two formulas are called linear combinations. More on linear combinations will be discussed on a different page.
We have seen that matrix multiplication is different from normal multiplication (between numbers). Are there some similarities? For example, is there a matrix which plays a similar role as the number 1? The answer is yes. Indeed, consider the nxn matrix



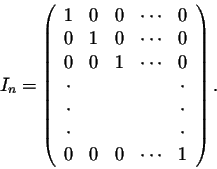
\begin{displaymath}I_n = \left(\begin{array}{ccccc} 1&0&0&\cdots&0\\ 0&1&0&\cdo... ...cdot\\ \cdot&&&&\cdot\\ 0&0&0&\cdots&1\\ \end{array}\right).\end{displaymath}



In particular, we have



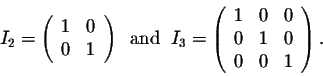
\begin{displaymath}I_2 = \left(\begin{array}{ccc} 1&0\\ 0&1\\ \end{array}\righ... ...egin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{array}\right).\end{displaymath}



The matrix In has similar behavior as the number 1. Indeed, for any nxn matrix A, we have



A In = In A = A



The matrix In is called the Identity Matrix of order n.
Example. Consider the matrices



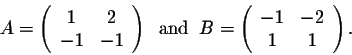
\begin{displaymath}A = \left(\begin{array}{cc} 1&2\\ -1&-1\\ \end{array}\right... ...B = \left(\begin{array}{cc} -1&-2\\ 1&1\\ \end{array}\right).\end{displaymath}



Then it is easy to check that



\begin{displaymath}AB = I_2 \;\;\mbox{and}\;\; BA = I_2.\end{displaymath}




The identity matrix behaves like the number 1 not only among the matrices of the form nxn. Indeed, for any nxm matrix A, we have



\begin{displaymath}I_n A = A\;\;\mbox{and}\;\; A I_m = A.\end{displaymath}



In particular, we have



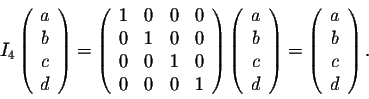
\begin{displaymath}I_4 \left(\begin{array}{c} a\\ b\\ c\\ d\\ \end{array}\ri... ... \left(\begin{array}{c} a\\ b\\ c\\ d\\ \end{array}\right).\end{displaymath}
Posted by

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)