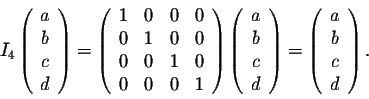01/16/12 ~ I Love Learning

Before we give the formal definition of how to multiply two matrices, we will discuss an example from a real life situation. Consider a city with two kinds of population: the inner city population and the suburb population. We assume that every year 40% of the inner city population moves to the suburbs, while 30% of the suburb population moves to the inner part of the city. Let I (resp. S) be the initial population of the inner city (resp. the suburban area). So after one year, the population of the inner part is

0.6 I + 0.3 S

while the population of the suburbs is

0.4 I + 0.7 S

After two years, the population of the inner city is

0.6 (0.6 I + 0.3 S) + 0.3 (0.4 I + 0.7 S)

and the suburban population is given by

0.4 (0.6 I + 0.3 S) + 0.7(0.4 I + 0.7 S)

Is there a nice way of representing the two populations after a certain number of years? Let us show how matrices may be helpful to answer this question. Let us represent the two populations in one table (meaning a column object with two entries):

$\begin{displaymath}\left(\begin{array}{c} I\\ S\\ \end{array}\right)\end{displaymath}$

So after one year the table which gives the two populations is

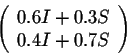
$\begin{displaymath}\left(\begin{array}{c} 0.6 I + 0.3 S\\ 0.4 I + 0.7 S\\ \end{array}\right)\end{displaymath}$

If we consider the following rule (the product of two matrices)

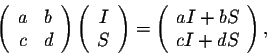
$\begin{displaymath}\left(\begin{array}{cc} a&b\\ c&d\\ \end{array}\right) \lef... ...left(\begin{array}{c} aI + bS\\ cI + dS\\ \end{array}\right),\end{displaymath}$

then the populations after one year are given by the formula

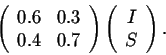
$\begin{displaymath}\left(\begin{array}{cc} 0.6&0.3\\ 0.4&0.7\\ \end{array}\right) \left(\begin{array}{c} I\\ S\\ \end{array}\right).\end{displaymath}$

After two years the populations are

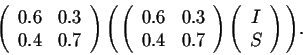
$\begin{displaymath}\left(\begin{array}{cc} 0.6&0.3\\ 0.4&0.7\\ \end{array}\rig... ...ght) \left(\begin{array}{c} I\\ S\\ \end{array}\right)\Bigg).\end{displaymath}$

Combining this formula with the above result, we get

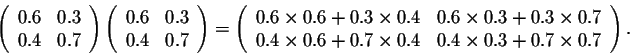
$\begin{displaymath}\left(\begin{array}{cc} 0.6&0.3\\ 0.4&0.7\\ \end{array}\rig... ...imes 0.4&0.4 \times 0.3 + 0.7 \times0.7\\ \end{array}\right). \end{displaymath}$

In other words, we have

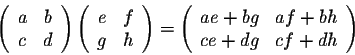
$\begin{displaymath}\left(\begin{array}{cc} a&b\\ c&d\\ \end{array}\right) \lef... ...{array}{cc} ae+ bg&af+bh\\ ce + dg&cf+dh\\ \end{array}\right)\end{displaymath}$

In fact, we do not need to have two matrices of the same size to multiply them. Above, we did multiply a (2x2) matrix with a (2x1) matrix (which gave a (2x1) matrix). In fact, the general rule says that in order to perform the multiplication AB, where A is a (mxn) matrix and B a (kxl) matrix, then we must have n=k. The result will be a (mxl) matrix. For example, we have

$\begin{displaymath}\left(\begin{array}{ccc} a&b&c\\ d&e&f\\ \end{array}\right)... ...a +b\beta +c\nu\\ d\alpha +e\beta +f\nu\\ \end{array}\right).\end{displaymath}$

Remember that though we were able to perform the above multiplication, it is not possible to perform the multiplication

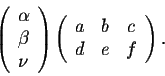
$\begin{displaymath}\left(\begin{array}{c} \alpha\\ \beta\\ \nu\\ \end{array}\... ...)\left(\begin{array}{ccc} a&b&c\\ d&e&f\\ \end{array}\right).\end{displaymath}$

So we have to be very careful about multiplying matrices. Sentences like "multiply the two matrices A and B" do not make sense. You must know which of the two matrices will be to the right (of your multiplication) and which one will be to the left; in other words, we have to know whether we are asked to perform $A \times B$ or $B \times A$ . Even if both multiplications do make sense (as in the case of square matrices with the same size), we still have to be very careful. Indeed, consider the two matrices

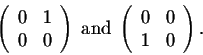
$\begin{displaymath}\left(\begin{array}{cc} 0&1\\ 0&0\\ \end{array}\right)\;\mb... ...nd}\; \left(\begin{array}{cc} 0&0\\ 1&0\\ \end{array}\right).\end{displaymath}$

We have

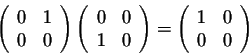
$\begin{displaymath}\left(\begin{array}{cc} 0&1\\ 0&0\\ \end{array}\right)\left... ...ht) = \left(\begin{array}{cc} 1&0\\ 0&0\\ \end{array}\right) \end{displaymath}$

and

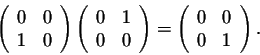
$\begin{displaymath}\left(\begin{array}{cc} 0&0\\ 1&0\\ \end{array}\right)\left... ...ht) = \left(\begin{array}{cc} 0&0\\ 0&1\\ \end{array}\right).\end{displaymath}$

So what is the conclusion behind this example? The matrix multiplication is not commutative, the order in which matrices are multiplied is important. In fact, this little setback is a major problem in playing around with matrices. This is something that you must always be careful with. Let us show you another setback. We have

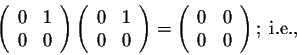
$\begin{displaymath}\left(\begin{array}{cc} 0&1\\ 0&0\\ \end{array}\right)\left... ...egin{array}{cc} 0&0\\ 0&0\\ \end{array}\right);\;\mbox{i.e.},\end{displaymath}$

the product of two non-zero matrices may be equal to the zero-matrix.

Properties involving Addition. Let A, B, and C be mxn matrices. We have

1.: A+B = B+A
2.: (A+B)+C = A + (B+C)
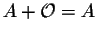
3.: $A + {\cal O} = A$
where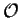 $\cal O$ is the mxn zero-matrix (all its entries are equal to 0);
4.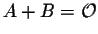: $A+B = {\cal O}$ if and only if B = -A.

Properties involving Multiplication.

1.: Let A, B, and C be three matrices. If you can perform the products AB, (AB)C, BC, and A(BC), then we have

(AB)C = A (BC)

Note, for example, that if A is 2x3, B is 3x3, and C is 3x1, then the above products are possible (in this case, (AB)C is 2x1 matrix).
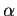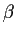2.: If $\alpha$ and $\beta$ are numbers, and A is a matrix, then we have

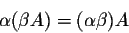
$\begin{displaymath}\alpha (\beta A) = (\alpha \beta) A\end{displaymath}$
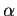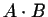3.: If $\alpha$ is a number, and A and B are two matrices such that the product $A\cdot B$ is possible, then we have

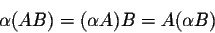
$\begin{displaymath}\alpha (AB) = (\alpha A)B = A (\alpha B)\end{displaymath}$
4.: If A is an nxm matrix and 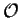$\cal O$ the mxk zero-matrix, then

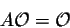
$\begin{displaymath}A {\cal O} = {\cal O}\end{displaymath}$

Note that $A {\cal O}$ is the nxk zero-matrix. So if n is different from m, the two zero-matrices are different.

Properties involving Addition and Multiplication.

1.: Let A, B, and C be three matrices. If you can perform the appropriate products, then we have

(A+B)C = AC + BC

and

A(B+C) = AB + AC
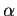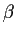2.: If $\alpha$ and $\beta$ are numbers, A and B are matrices, then we have

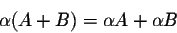
$\begin{displaymath}\alpha (A+B) = \alpha A + \alpha B\end{displaymath}$

and

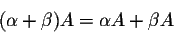
$\begin{displaymath}(\alpha +\beta)A = \alpha A + \beta B\end{displaymath}$

Example. Consider the matrices

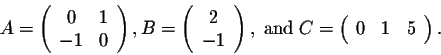
$\begin{displaymath}A = \left(\begin{array}{cc} 0&1\\ -1&0\\ \end{array}\right)... ...nd}\; C = \left(\begin{array}{ccc} 0&1&5\\ \end{array}\right).\end{displaymath}$

Evaluate (AB)C and A(BC). Check that you get the same matrix.
Answer. We have

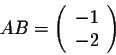
$\begin{displaymath}AB = \left(\begin{array}{c} -1\\ -2\\ \end{array}\right)\end{displaymath}$

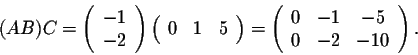
$\begin{displaymath}(AB)C = \left(\begin{array}{c} -1\\ -2\\ \end{array}\right)... ...t(\begin{array}{ccc} 0&-1&-5\\ 0&-2&-10\\ \end{array}\right).\end{displaymath}$

On the other hand, we have

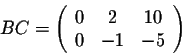
$\begin{displaymath}BC = \left(\begin{array}{ccc} 0&2&10\\ 0&-1&-5\\ \end{array}\right)\end{displaymath}$

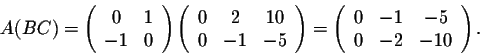
$\begin{displaymath}A(BC) = \left(\begin{array}{cc} 0&1\\ -1&0\\ \end{array}\ri... ...t(\begin{array}{ccc} 0&-1&-5\\ 0&-2&-10\\ \end{array}\right).\end{displaymath}$

Example. Consider the matrices

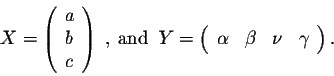
$\begin{displaymath}X = \left(\begin{array}{c} a\\ b\\ c\\ \end{array}\right)\... ...ray}{cccc} \alpha & \beta & \nu & \gamma\\ \end{array}\right).\end{displaymath}$

It is easy to check that

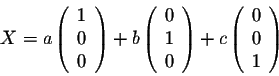
$\begin{displaymath}X = a \left(\begin{array}{c} 1\\ 0\\ 0\\ \end{array}\right... ...) + c \left(\begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right) \end{displaymath}$

and

$\begin{displaymath}Y = \alpha \left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ \end{ar... ...ma \left(\begin{array}{cccc} 0 &0 & 0& 1\\ \end{array}\right).\end{displaymath}$

These two formulas are called linear combinations. More on linear combinations will be discussed on a different page.
We have seen that matrix multiplication is different from normal multiplication (between numbers). Are there some similarities? For example, is there a matrix which plays a similar role as the number 1? The answer is yes. Indeed, consider the nxn matrix

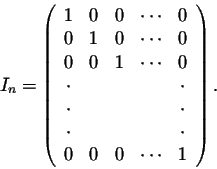
$\begin{displaymath}I_n = \left(\begin{array}{ccccc} 1&0&0&\cdots&0\\ 0&1&0&\cdo... ...cdot\\ \cdot&&&&\cdot\\ 0&0&0&\cdots&1\\ \end{array}\right).\end{displaymath}$

In particular, we have

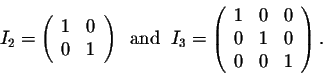
$\begin{displaymath}I_2 = \left(\begin{array}{ccc} 1&0\\ 0&1\\ \end{array}\righ... ...egin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{array}\right).\end{displaymath}$

The matrix I_n has similar behavior as the number 1. Indeed, for any nxn matrix A, we have

A I_n = I_n A = A

The matrix I_n is called the Identity Matrix of order n.
Example. Consider the matrices

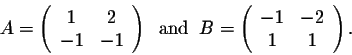
$\begin{displaymath}A = \left(\begin{array}{cc} 1&2\\ -1&-1\\ \end{array}\right... ...B = \left(\begin{array}{cc} -1&-2\\ 1&1\\ \end{array}\right).\end{displaymath}$

Then it is easy to check that

$\begin{displaymath}AB = I_2 \;\;\mbox{and}\;\; BA = I_2.\end{displaymath}$

The identity matrix behaves like the number 1 not only among the matrices of the form nxn. Indeed, for any nxm matrix A, we have

$\begin{displaymath}I_n A = A\;\;\mbox{and}\;\; A I_m = A.\end{displaymath}$

In particular, we have

$\begin{displaymath}I_4 \left(\begin{array}{c} a\\ b\\ c\\ d\\ \end{array}\ri... ... \left(\begin{array}{c} a\\ b\\ c\\ d\\ \end{array}\right).\end{displaymath}$

I Love Learning

Mulailah

Semangat

Konsisten

Pantang Menyerah

Be The One

Monday, January 16, 2012

Matrix Operations

m-edukasi

Users Online

Feedjit

Link sahabat

Coretan Tangan

BERITA

Blogroll

Blogger templates

Kumpulan Tulisan